 login/create account
login/create account
polytope, projection, extension complexity, convex polygon
Extension complexity of (convex) polygons ★★
Author(s):
The extension complexity of a polytope 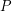 is the minimum number
is the minimum number 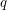 for which there exists a polytope
for which there exists a polytope 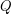 with
with 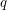 facets and an affine mapping
facets and an affine mapping  with
with 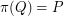 .
.
Question Does there exists, for infinitely many integers  , a convex polygon on
, a convex polygon on  vertices whose extension complexity is
vertices whose extension complexity is 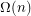 ?
?
 , a convex polygon on
, a convex polygon on  vertices whose extension complexity is
vertices whose extension complexity is 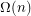 ?
? Keywords: polytope, projection, extension complexity, convex polygon

 Drupal
Drupal CSI of Charles University
CSI of Charles University