 login/create account
login/create account
Conjecture Let 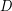 be the open unit disk in the complex plane and let
be the open unit disk in the complex plane and let 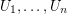 be open sets such that
be open sets such that 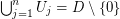 . Suppose there are injective holomorphic functions
. Suppose there are injective holomorphic functions 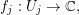
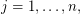 such that for the differentials we have
such that for the differentials we have 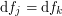 on any intersection
on any intersection 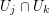 . Then those differentials glue together to a meromorphic 1-form on
. Then those differentials glue together to a meromorphic 1-form on 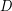 .
.
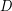 be the open unit disk in the complex plane and let
be the open unit disk in the complex plane and let 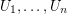 be open sets such that
be open sets such that 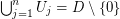 . Suppose there are injective holomorphic functions
. Suppose there are injective holomorphic functions 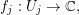
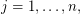 such that for the differentials we have
such that for the differentials we have 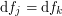 on any intersection
on any intersection 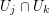 . Then those differentials glue together to a meromorphic 1-form on
. Then those differentials glue together to a meromorphic 1-form on 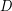 .
. It is an evidence that the 1-form is holomorphic on  . In the case that its residue at the origin vanishes we can use Picard's big theorem.
. In the case that its residue at the origin vanishes we can use Picard's big theorem.
Bibliography
*B. Elsner: Hyperelliptic action integral, Annales de l'institut Fourier 49(1), p.303–331
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University