 login/create account
login/create account
Conjecture Every planar linear hypergraph 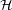 has a straight line representation in the plane which maps each vertex
has a straight line representation in the plane which maps each vertex  to a point
to a point 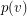 and each edge
and each edge 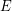 to a straight line segment
to a straight line segment 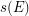 , in such a way that:
, in such a way that:
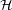 has a straight line representation in the plane which maps each vertex
has a straight line representation in the plane which maps each vertex  to a point
to a point 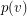 and each edge
and each edge 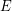 to a straight line segment
to a straight line segment 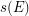 , in such a way that:
, in such a way that:- \item for each vertex
 and each edge
and each edge 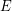 , we have:
, we have: 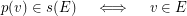 \item for each couple of distinct edges
\item for each couple of distinct edges 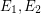 , we have
, we have 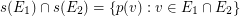
Bibliography
*[dFOdM] Hubert de Fraysseix, Patrice Ossona de Mendez: Stretching of Jordan arc contact systems, Discrete Applied Mathematics 155 (2007), no. 9, 1079--1095.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University