I haven't worked through the details yet, but what if is the union of and a sufficiently huge bipartite graph ? Then , and by taking huge enough, you can get as close to 2 as you like, forcing as small as you like.
EDIT: Whoo boy. Nevermind.
No?
I haven't worked through the details yet, but what if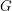 is the union of
is the union of 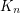 and a sufficiently huge bipartite graph
and a sufficiently huge bipartite graph 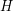 ? Then
? Then 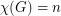 , and by taking
, and by taking 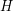 huge enough, you can get
huge enough, you can get 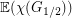 as close to 2 as you like, forcing
as close to 2 as you like, forcing  as small as you like.
as small as you like.
EDIT: Whoo boy. Nevermind.