 login/create account
login/create account
Strong colorability
Let  be a positive integer. We say that a graph
be a positive integer. We say that a graph  is strongly
is strongly  -colorable if for every partition of the vertices to sets of size at most
-colorable if for every partition of the vertices to sets of size at most  there is a proper
there is a proper  -coloring of
-coloring of  in which the vertices in each set of the partition have distinct colors.
in which the vertices in each set of the partition have distinct colors.
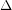 is the maximal degree of a graph
is the maximal degree of a graph  , then
, then  is strongly
is strongly 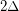 -colorable.
-colorable. Haxell proved that if 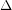 is the maximal degree of a graph
is the maximal degree of a graph  , then
, then  is strongly
is strongly 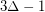 -colorable. She later proved that the strong chromatic number
-colorable. She later proved that the strong chromatic number 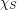 is at most
is at most 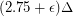 for sufficiently large
for sufficiently large 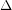 depending on
depending on  . Aharoni, Berger, and Ziv proved the fractional relaxation.
. Aharoni, Berger, and Ziv proved the fractional relaxation.
Problem Solved!
See "On the Strong Chromatic Number of Graphs" by Maria Axenovich and Ryan Martin (2006)
only partly solved
The paper cited (available at http://orion.math.iastate.edu/axenovic/Papers/Martin_Strong.pdf) only resolves the above conjecture for graphs G which have maximum degree at least |V(G)|/6.
That theorem has been proved
That theorem has been proved in an even older paper by another set of authors.
After a quick search I found that paper at http://abel.math.umu.se/~klasm/Uppsatser/factor.pdf
still only a partial solution
Once again, the paper cited offers only a partial solution. Quoting from the paper, "From Theorem 1.1, we conclude that the strong chromatic number can be bounded by 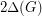 if
if 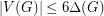 . This result should not be compared with the more complete and difficult result of Alon." Here, the difficult result of Alon is the theorem that there exists a fixed constant
. This result should not be compared with the more complete and difficult result of Alon." Here, the difficult result of Alon is the theorem that there exists a fixed constant 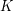 so that every graph of maximum degree
so that every graph of maximum degree 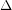 is strongly
is strongly 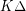 -colorable.. precisely the result which is sharpened by this conjecture.
-colorable.. precisely the result which is sharpened by this conjecture.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Recent progress
Haxell proved that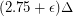 is sufficient for sufficiently large
is sufficient for sufficiently large 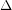 depending on
depending on  . (JGT, 2008)
. (JGT, 2008)
Aharoni, Berger, and Ziv proved the fractional relaxation, i.e. that with partition cliques of size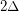 we have a fractional
we have a fractional 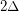 colouring. (Combinatorica, 2007)
colouring. (Combinatorica, 2007)